Chapter 12: Bit Manipulation
At their core, computers are all about data and represent all data as binary bits. C has several powerful features that allow us to manipulate data at the bit level. This chapter will discuss how to work with binary data and the C features that manipulate that data.
All Data Are Binary
Before we get started with with bits and binary operations, we should note that all data are binary.
While this may seem like a very simple statement, it needs mentioning. It is often tempting to think of "converting" data to binary in a program before we use it. For example, if we declare a variable to be an integer or a character, it is easy to make the mistake that we must somehow convert that variable to binary before we manipulate it.
The truth is that all numbers, all structured data, all collections, are binary. Binary is the only way to represent data in a computer's volatile or non-volatile storage. This means that bitwise binary operators that we will discuss in this chapter are applicable to all pieces of data, no matter how they are declared or used.
Now that we have stated this, we should also state that it does not make sense to use binary operations on everything. Consider this example.
int datumi;
float datumf;
datumf = 12.6;
datumi = (int) datumf;
It indeed true that datumf is stored in memory as binary and in IEEE 754 format for floating point numbers. But because the C programming language uses higher level abstraction to represent data, the exact binary sequence that represents datumf is not directly available in the above code. All that we can do with assignment is to cast datumf to an integer, which is defined to truncate the value at the decimal point. We cannot, for example, extract just the mantissa or just the exponent through bitwise operations (although we can do this through unions, as we will show in a section below).
This means that data that can be represented as integers or that can be cleanly and completely cast to integers can be manipulated with bitwise operations. While it does not make sense to use bitwise operators on all data, we can, as we will see, manipulate any data object using unions.
Standard Bitwise Operators
We have described "true" values as compatible with the integer value 1 and "false" values as compatible with the integer value 0. This analogy also helps with bitwise arithmetic.
Translating "true" to 1 and "false" to 0, we can rewrite our boolean / logical operations as bitwise arithmetic operations, as below:
| Operator Name | Syntax | Meaning |
| AND | a & b | Result is true when both operands are true |
| OR | a | b | Result is true when at least one of the operands is true |
| XOR | a ^ b | Result is true when exactly one of the operands is true |
| NOT | ! a | Result is true when the operand is false; result is false when the operand is true |
Bitwise operators do their work on the individual bits on integer values. A number may have the integer decimal value of "72", but the binary representation is (in 8 bits) "01001000". When we perform bitwise operations on integers, we are focused on the binary representation, not the decimal representation.
Let's look at some examples.
char pattern1 = 0b100101;
char pattern2 = 0b1001;
char pattern3 = pattern1 & pattern2;
char pattern4 = pattern1 | pattern2;
char pattern5 = ! pattern4;
char pattern6 = pattern1 ^ pattern2;
First note that we have declared these patterns to be of the type char, which represents 8 bits. Second, note that these bit patterns (we know they are bit patterns because they start with the "0b" prefix) are indeed integer values. pattern1 has the decimal value 37 and pattern2 has the decimal value 9. This means that the value of pattern3 is 1:
100101
& 1001
--------
000001
and the value of pattern4 is a decimal 45:
100101
| 1001
--------
101101
By complementing the bits of pattern4, pattern5 gets a binary value of 11111111111111111111111111010010 for a 32 bit integer, which is a decimal value of -46 (using 2's complement representation of negative numbers, which is what C does).
The ^ operator makes pattern6 in the example above has the value 101100, calculated as follows:
100101
^ 1001
--------
101100
Two's Complement Negative Representation
Negative numbers need to be represented in an integer just like positive numbers. 2's complement is an encoding method that represents negative numbers such that integer arithmetic works like it should without special considerations.
The 2's complement representation of a negative number works like this: if a number is negative, complement all bits in the number and add the value
1. For example,20has an 8-bit binary representation of00010100, so-20has an 8-bit representation of11101100, calculated as:20<sub>10</sub> = 0b00010100 -20<sub>10</sub> = !0b00010100 + 1 = 0b11101011 + 1 = 0b11101100This method of representing negative numbers has some implications of number ranges that can be represented. Unsigned integers that are n bits long can represent numbers from 0 to 2n-1. 2's complement negative representation splits that range into two parts, negative and positive, and therefore the maximum positive integer that can be represented is half of that for unsigned integers: -2n-1 to 2n-1-1. So a 32-bit computer can represent integers from -2,147,483,648 to 2,147,483,647.
As with other operations, C combines bitwise operations with the assignment operator. Each of and, or, and xor has an assignment abbreviation: &=, |=, and ^=.
Shifting Operators
In addition to bitwise operators, C also includes operators to shift entire bit sequences.
Bits can be shifted right or left for a specific number of positions. The operator << shifts left and the operator >> shifts right. Shift operators only work on integers, although casting is performed first if the operand is a compatible type. Let's consider an example:
int pat1 = 10, pat2 = 0b101100;
int pat3, pat4;
pat3 = pat1 << 4;
pat4 = pat2 >> 3;
In this example, pat3 now has the value 160. When the value of pat1, which is 1010 in binary, gets shifted 4 bits left, the result is 0b1010000, which is a decimal 160. pat4 is assigned the value 5, which is 0b101100 shifted right 3 bits, resulting in the binary 0b000101, or simply 0b101.
Consider another example:
short int pat5 = 0b1111111100010000;
pat5 = pat5 << 8;
This example demonstrates that left shifting is logical shifting. The bits shifted off to the left are discarded. The bits shifted in from the right are 0. The value of pat5 in this example ends up to be 0b0001000000000000 when discarding the 8 leftmost bits.
However, shifting right is actually an arithmetic shift. Arithmetic shifting preserves the sign bit and does not consider the leftmost bit part of the bit sequence is eligible to be shifted. In the example above, pat5 is initialized to have the value -240 and has the value 4096 after shifting left. But if we were to shift the original value right 8 bits, we would get 0b1111111111111111, which is a -1 in 2's complement.
Some programming languages include a circular shift operator. Also known as rotation, circular shifting takes the bits shifted off and inserts them in the opposite side of the bit sequence. If the left shift in the above example had been a circular shift, the result in pat5 would have been 0b0001000011111111 in binary or 4351 in decimal.
There is no circular shift operator in C. However, we can implement circular shifting in C using the function below:
int leftrotate(int original, int numbits) {
return (original << numbits) | (original >> (sizeof(original)*8 - numbits));
}
For example, if we wanted to use a circular shift for the example above, we would call leftrotate(pat5, 8). It would return
(0b1111111100010000 << 8) | (0b1111111100010000 >> (16 - 8))
= 0001000000000000 | 0000000011111111 = 0001000011111111
We could write a similar function for rotating right.
Shifting Implements Multiplication and Division
If we use an arithmetic shift, shifting left 1 bit is actually the equivalent to multiplying by 2. Analogously, shifting right is division by 2. Multiple bit shifts are equivalent to multiplying or dividing by powers of 2.
Multiplication and division are very complicated and time-consuming when compared to shifting. In fact, compilers will often turn multiplications and divisions into shifts and additions or subtractions.
Higher Level Operations with Bits
While it is useful to be able to use basic bitwise arithmetic, we can build these bitwise operators into higher level, more abstract, operations. These include extraction, inverting, clearing, and setting spans of bits inside a number. Each of these operations requires a binary operator and a mask, or pattern, of bits.
Extraction is the operation of creating a new bit sequence comprised of the bits taken from certain bit positions in the operand and 0 values for the other positions. This requires an and operation and a mask with 1 values in the positions we want to extract. For example, consider the code below:
short int bitstring1 = 0b1010000111110010;
short int mask1 = 0b1111111100000000;
short int extraction = bitstring1 & mask1;
Here, we have an extraction operation that extracts the leftmost 8 bits from the bitstring1 variable. The value of extraction therefore is 1010000100000000.
An invert operation complements specific bit in an operand and ignores the rest of the bits. This needs an xor operation with a mask where 1 values mark the positions to invert and the 0 values mark the positions to ignore. Here is an example:
short int bitstring2 = 0b1010101000011110;
short int mask2 = 0b0000111111110000;
short int inversion = bitstring2 ^ mask2;
In this example, we are inverting the middle 8 bits of this 16 bit sequence. The resulting value of inversion is 1010010111101110.
A clear operation turns certain specific bit positions in the operand to 0. The operation is an and and the mask uses 0 values on the positions to clear, with 1 values everywhere else. Consider this example:
short int bitstring3 = 0b1111010100001010;
short int mask3 = 0b0000111111111111;
short int clearing = bitstring3 & mask3;
This example clears the leftmost 4 bits, giving clearing the value 0000010100001010.
As you might expect, a setting operating does the opposite of clearing. It sets specific bits to 1. The operation is an or and the mask puts 1 values on the positions to set, with 0 values elsewhere. Here's one more example:
short int bitstring4 = 0b0000110100001010;
short int mask4 = 0b0000111111110000;
short int setting = bitstring4 | mask4;
This example makes sure that the middle 8 bits are set, resulting in setting having the value 0000111111111010.
Let's consider one more example here. If a programmer wants to make an app that responds to time events, then the TickTimerService needs to be used. This service be configured to call a handler function every time a specific Time component changes. This is very important for watchfaces. In order to subscribe to the TickTimerService, you must construct a bitmask of the units you are interested in. For example, let's say we want to call a TickTimerService handler function every minute. We might execute code like this:
short int mask = MINUTE_UNIT;
tick_timer_service_subscribe(mask, tick_handler);
This code assumes that tick_handler exists. An example of a tick handler is below:
void tick_handler(struct tm *tick_time, TimeUnits units_changed) {
short int minutes_changed = units_changed & MINUTE_UNIT;
short int hours_changed = units_changed & HOUR_UNIT;
if (minutes_changed) { ... }
if (hours_changed) { ... }
}
This code checks to see if the minutes changed and the hours changed. Because we suscribed to the TickTimerService with the mas MINUTE_UNIT, we can probably assume that the minutes unit has changed. But the hours might have changed as well and we can use bit extraction to test that.
For a more detailed discussion of the TickTimerService, including and examination of the TimeUnits enum type, see Chapter 14.
Bit Fields
A discussion of bit manipulation should include a mention of the topic of bitfields. Bitfields are limited in their usefulness, but deserve a look.
A bitfield is part of a struct or union declaration that restricts the storage space for the variable being declared to a specific number of bits. Consider this example:
struct {
int bfield1 :8;
int bfield2 :4;
unsigned :4;
unsigned bfield3 :2;
signed int bfield4 :1;
} fields;
fields.bfield1 = 40;
fields.bfield2 = fields.bfield1 - 20;
fields.bfield3 = 5;
Bitfields are specified with a colon and the number of bits the variable is supposed to be allocated. In the above example, fields.bfield1 is declared to be 8 bits wide. The variable is signed and so may take on values -128 to 127 (remember 2's complement). In this example, fields.bfield2 is given 4 bits and is signed. It is assigned the value 20, but that value is truncated to the rightmost 4 bits, giving the value 4 (the value 0b10100 is truncated to 0b0100). The last statement in the example would actually be flagged as an error by the compiler; the compiler can see that a variable that has only 2 bits allocated to it cannot take on the value 5.
Note the declaration in the example that has a type name without a variable name. The declaration between bfield2 and bfield3 can take up space and skip over bits with being assigned a value. It's a kind of padding specification.
Bitfields and padding declarations are more useful when they are used with unions. Consider this example:
union {
unsigned short data;
struct {
unsigned x :4;
unsigned y :4;
unsigned :2;
unsigned z :4;
unsigned :2;
};
} dfields;
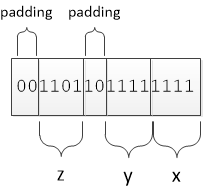
dfields.data = 14079;
The integer value 14079 can be represented in binary as 0b0011011011111111. By assigning dfields.data to this value, we can lay the struct on top of this bit sequence and carve up the bits. But here is where the word of warning we mentioned in Chapter 10 comes to play: because the processor used in Pebble smartwatches is big-endian, the values are assigned right to left. x gets the value 15; y has the value 15, and z has the value 13. Notice that the padding specification are useful here to put some "bit space" between y and z. Figure 12.1 illustrates how the original integer value was split up.
The Utility of Unions and Binary Data
The previous section pointed out one place where unions are useful: binary data and bitfields. Assembling bit sequences that are made up of segments of other binary data can be tedious and cryptic with binary operations, but much easier with unions.
Let's consider an example. Let's say that we invent an "encryption" for a letter by rotating that letter through the alphabet (this was invented long ago; it's called a Ceasar cipher). 'A' might be rotated by 5 to become 'F'; 'd' might be rotated by 10 to become 'n'; 'y' might be rotated by 5 around to the beginning of the alphabet at 'c'. We might transfer data encrypted this way by packing the code with the rotation like this:

We might pack this using C code in the following way:
int packed = rotation << 5 | character;
Specifying this with a union would be clearer:
union code_format {
short unsigned rotation :5;
short unsigned character :8;
};
We only need 5 bits for rotation because 26 (maximum rotation) can be encoded in 5 bits.
We would pack a character like this:
union code_format packed;
packed.rotation = 10;
packed.character = 'n';
The code is longer, but the meaning is clearer.
Coding with color definitions shows this off in a big way, as we see in the next section.
Putting Bit Operations to Work: Color Manipulation
Let's look at how bit manipulation can be used with color.
The usual standard for color representation is a combination of red, green, and blue values, each taking 8 bits. These values are put together with a measure of transparency, called an "alpha" measure, which is also 8 bits. This results in 32 bits, with 256 values possible for each red, green, blue, and alpha values, which results in millions of possible colors.
However, the Pebble smartwatch screen has 64 different possible colors, not millions. This means that we only need 6 bits to represent the color: 2 bits for each of red, green, and blue values. If we add 2 bits for transparency, we're able to represent Pebble's full spectrum of available colors using only 8 bits instead of 32. Here is the definition of GColor8, the 8-bit color representation:
typedef union GColor8 {
uint8_t argb;
struct {
uint8_t b:2; //!< Blue
uint8_t g:2; //!< Green
uint8_t r:2; //!< Red
uint8_t a:2; //!< Alpha.
};
} GColor8;
As we described the screen's color needs, there are 2 bits for each base color and 2 bits for the transparency value. With this definition, the GColor definition is made equivalent to this 8 bit representation with a typedef statement:
typedef GColor8 GColor;
But we still have standard, 32-bit RGB color specifications. So the Pebble SDK defines some conversion code. For example, GColorFromRGBA(red, green, blue, alpha) is defined as
((GColor8){ \
.a = (uint8_t)(alpha) >> 6, \
.r = (uint8_t)(red) >> 6, \
.g = (uint8_t)(green) >> 6, \
.b = (uint8_t)(blue) >> 6, \
})
(Ignore the '\' character for now; this definition is actually a macro definition and we will discuss macros in a future chapter on the C preprocessor. Also remember that uint_8 is an 8-bit unsigned integer type.)
This example shows that 32-bit to 8-bit conversion is done by taking the most significant bits of each color (losing the other bit by shifting right 6 bits) and assembling the resulting bit pattern through the union. The Pebble SDK also defines an RGB value without an alpha part to be a color specification with the alpha designation completely opaque, as below:
GColorFromRGBA(red, green, blue, 255);
Let's look at a conversion example. According to the color picker tool in the Pebble documentation (available here), the color "Jaeger Green" is comprised of no red, with green having a value of 170 and blue having a value of 85. To convert these value to a Pebble screen color, we would make the following call:
GColor jaeger_green = GColorFromRGB(0, 170, 85);
This is equivalent to the following code:
GColor jaeger_green = (GColor8){ .a = 255 >> 6, .r = 0 >> 6, .g = 170 >> 6, .b = 85 >> 6 };
This, in turn, is equivalent to
GColor jaeger_green = (GColor8){ .a = 0b11111111 >> 6, .r = 0b00000000 >> 6,
.g = 0b10101010 >> 6, .b = 0b01010101 >> 6 };
This turns into
GColor jaeger_green = (GColor8){ .a = 0b11, .r = 0b00, .g = 0b10, .b = 0b01 };
And this is equivalent to
GColor jaeger_green = (GColor8){ .argb = 201 };
because 0b11001001 is 201 decimal.
Avoiding Messy Bit Operations
Working with bits can get messy quickly when we start combining operators and abbreviated notation. Here's a few tips to making bitwise opeartions as clear as possible.
Use names for values whenever possible rather than literals. Colors are great example here. The name "Jaeger Green" is much more descriptive than "201" or "GColorFromRGB(0, 170, 65)" or "0b11001001". Naming values with names that depict how they are used is a very good habit to have.
Use names for values affecting shifting and bit positions. This means that naming the position values when shifting or masking makes more sense than simply using an integer literal. It's much clearer to use something like
extraction = bitstring1 & mask1;than it is to usebitstring &= 240;.Use whitespace to align bits in expressions. This may seem silly or not necessary, but when using bits expressed literally, use bitwise notation ("0b...") and use whitespace to align values in operations. It is much easier (and more meaningful) to work with columns of operations when the bits are aligned.
Use unions with bitfields as documentation and easy conversion tools. Unions with bitfields are extremely valuable to document the format of data and to facilitate easy conversion between values. It's clearer when reading data values to use a union to split the data into component pieces than it is to work with shifting and bitwise operators.
Project Exercises
Project 12.1
Recall that we did an example in this chapter involving Ceasar ciphers: rotating letters through the alphbet. We described a possible format for letters in an "encryption": the rotation number in the leftmost 8 bits and the actual letter in the rightmost 8 bits. We actually don't need 8 bits to represent rotation, 5 bits will be able to represent 0 through 25 values of rotation.
You are to read a file of numbers that are specified using this "Ceasar Cipher Format" (CCF) notation: 5 bits of rotation followed by 8 bits of character representation. You are to translate the message in file and display it on the Pebble screen.
You can find starter code here. The starter code reads the file of numbers, which are encoded letters (they form a message). The code implements a function called get_decoded_line that gets a sentence from the file and decodes it. This function calls decode_next_letter for each letter in the message. Look for this function. It will give you the next encoded CCF letter from the file and decodes it. You are fill this definition in. Note the parameters. The position is passed as a pointer to an integer so it can change (why?).
Project 12.2
For this project, you will take the starter code (available here) and add code to fill in the screen of the Pebble in color gradations from GColorBlack (0b11000000) to GColorWhite (0b11111111). Vertically or horizontally, you should be able to go through two gradation sequences.
There are several ways to work through the colors here. From simple addition to manipulation of colors through unions, you should be able to implement different methods. Use at least two to have the same gradation effect.
You can find an answer using several gradation implementations here. The code is currently set up to use the first defined code. Change the definition
#define USE_METHOD_ONE
to
#undef USE_METHOD_ONE
to use the second algorithm.
Project 12.3
Find the starter code for this project here.
For this project, you are going to tie Pebble screen color changes to button presses. The "up" button should manipulate red; the "select" button should manipulate green; the "down" button should manipulate blue. Each button will cycle through all values for it's assigned color; there are only 4 values for each one.
Start the screen background with a GColorBlack color. Change the background based on the values of red, green, and blue given by button presses.
Like the previous project, there are several ways to implement this. The best way, however, is to maintain a color value for each color and build the background color from the three base color values and a fixed transparency.